| prev |
CHAPTER III |
next |
Salmon suggests that Zeno is not just putting paradoxes forth.
It has been suggested, and Owen elaborates this theme, that Zeno's arguments fit into an overall pattern. "Achilles and the tortoise" and "The dichotomy" are designed to refute the doctrine that space and time are continuous, while "The arrow" and "The stadium" are intended to refute the view that space and time have an atomic structure.(1)
The pattern suggested by Owen suggests a Zen koan -- a parable with illustrative value that is often logically inconsistent. Such parables are used to stimulate a disciple toward certain realizations, and a perennial theme of Zen koans is that obvious choices should be rejected. In this case the choice is between atomism and infinite divisibility. Heraclitus rejected such a choice in his doctrine of the unity of opposites. Zeno's arguments, purporting to refute both choices, seem compatible with Heraclitus. But, as with Zen, many disciples never master the teachings; some write long dissertations arguing pro or con regarding some illustrative parable. Regarding oneness or manyness -- atomism or infinite divisibility -- many such dissertations have been written.
Zeno confuses discrete and dense sets, and he assumes that zero times infinity is zero. These errors figure prominently in his arguments. In a sense, 'discrete' means atomic and 'dense' means divisible. (See page 100.) Today we are accustomed to distinguishing between these two kinds of sets. Certain properties or attributes are associated with each kind of set. For example, the notion expressed by 'next' or 'successor' is one from counting and is associated with discrete (atomic) sets. Whenever one asks about the next one of any sequence, one is introducing the atomic perspective into the discussion. We have mathematical models of both kinds of sets. The integers are discrete; the rational (and real) numbers are dense. Both numbering systems are applied to extension, as Aristotle notes. (See page 91.) Metric space theory allows discrete as well as continuous measures of extension. But continuous metrics are far more well known than discrete metrics.
In "Achilles and the Tortoise", Max Black suggests that the paradox derives from an imprecise use of language.
[The] fallacy in Zeno's argument is due to the use of the words 'never' and 'always'."(2)
But Black does not expand and make explicit his assertion. Instead, he suggests that an infinite series of acts is self-contradictory. Black is guilty of exactly the charge he levies, only with a different word. It is not the infinite series of acts that is problematical; it the notion of completing an infinite series of acts on a one-at-a-time basis. Black's statement, "the machine comes to a halt", suggests this sense.(3) The sense of completion involving a one-at-a-time process presumes that there is an end to the process, whereas Peano's successor axiom presumes that there is no end to the process (of counting natural numbers). If complete is understood in this sense, then "completing" an infinite series of tasks means "coming to the end of a sequence with no end", which is indeed self-contradictory.
For it is the very essence of [an infinite] progression not to have a last term and not to be completable in that ordinal sense! To maintain the self-contradictory proposition that in such an actually infinite aggregate of order type , there is a "last" set of divisions which ensure the completability of the process of "infinite division" by "reaching" a "final" product of division is indeed to commit the Bernoullian fallacy.(4)
But there is another sense of complete which must be used while scrupulously avoiding the sense which connotes coming to an end.(5) That sense is expressed by "all there". For finite sets, and in ordinary usage, both senses apply at the same time. In fact, one discovers whether the silverware is "all there" by counting it and coming to the (right) end. When we distinguish between these two senses of complete, we see that we cannot apply both senses to an infinite set. An infinite series of acts, or an infinite set of numbers, is complete in the sense that all acts, or numbers, are included, while it simultaneously fails to be complete in the sense of coming to an end. Finite sets may be distinguished from infinite sets by examining whether the sense of "complete" expressed by 'coming to an end' applies. Black fails to make this distinction.
If we follow-up on Black's imprecise lead we can see that 'always' is used in a particular way in Zeno's argument. It can be properly represented as meaning "for all N". In the form of the argument expressed by Black, Achilles runs at the speed of 10 yards per second, while the tortoise runs at 1 yard per second and is given a 100 yard head start. (Achilles has a 100 yard handicap.) If Achilles runs at 10 yards per second and the tortoise has a 100 yard head start, then Achilles will take 10 seconds to arrive at the spot vacated by the tortoise. (100 Yd /10 Yps = 10 sec.) In that 10 seconds, the tortoise, who runs at 1 yard per second, will have run 10 yards. So, according to this form of the paradox, while Achilles runs the 100 yard handicap, the tortoise has run another 10 yards. This puts the tortoise 10 yards ahead of Achilles. We can think of the race as starting again with a 10 yard handicap. While Zeno runs the 10 yards the tortoise runs one yard.
Let us assign N=1 to the first race and N=2 to the second race. Naturally, there is a third race, and a fourth, etc., etc. In the first race Achilles runs 100 yards; in the second race he runs 10 yards; and in the third race he runs 1 yard. This sequence can be expressed in exponential form as 102, 101, 100, . The relationship between the distance and the race number can be more clearly seen if we express the sequence as 10(3-1), 10(3-2), 10(3-3), . . . . We can compute the distance run in each race by Achilles if we use the expression 10(3-N), where N is the race number. The tortoise, on the other hand, travels at 1/10 the speed of Achilles. In the 10 second first race he travels 10 yards; in the 1 second second race he travels 1 yard; in the .1 second third race he travels .1 yard. The corresponding sequence for the tortoise is 10(2-1), 10(2-2), 10(2-3), . . . . We can compute the distance run in each race by the tortoise if we use the expression 10(2-N).
By the same reasoning we can discover an expression for the distance between Achilles and the tortoise after each race. After the first race the tortoise is ahead by 10 yards; after the second race by 1 yard, and so forth. Each term in the sequence, 101, 100, 10-1, . . . , can be computed using the expression 10(2-N). This is the same as the amount the tortoise runs, and this makes sense because it is the amount the tortoise runs that puts him ahead of Achilles. Now, it is quite clear that this number is a positive quantity for every N. Since there is never an end to numbers, it is usually concluded that Achilles can never come to the end of the races, that is, Achilles can never catch the tortoise. That there is never an end to numbers is perhaps better stated by Peano's successor axiom: every number has a successor. In the present context we should not conclude that Achilles can never catch the tortoise; rather, we should conclude that for every N, the tortoise has a 10(3-N) yard lead on Achilles." While this can be paraphrased as: "the tortoise is 'always' ahead of Achilles" and subsequently re-paraphrased as "Achilles can 'never' catch the tortoise", it is usually forgotten that the 'always' and 'never' are limited by the original context to the integers which index the successive races. The more general sense of 'always' -- "for all time" ('never' -- "at no time") dominates our understanding of the final paraphrase. The argument, in effect, equivocates between two meanings of 'always' or 'never'.
Were we to 'extend' the integers by adding the axiom of infinity, without explaining how Achilles might "complete" the finite races, trans-finite races would place Achilles at, and beyond, the location of the tortoise. But the axiom of infinity essentially assumes that the number infinity exists. In the context of the Achilles, that is tantamount to assuming that Achilles catches the tortoise.
There is a subtle fallacy at work in the argument. It can be illustrated by an analogy. Gödel's incompleteness theorem showed that arithmetic is essentially incomplete. That is, true statements can be constructed in arithmetic which are formally undecidable on the basis of the given axioms. While an undecidable statement may be added as an axiom, the extended system so created is also incomplete.(6) As noted above, "nothing in these premisses allows us to conclude that Achilles actually catches the tortoise." The statement "Achilles catches the tortoise", is not decidable on the basis of the premisses and inferences given for The Achilles. It is, of course, true that Achilles catches the tortoise. Like Gödel's constructed undecidable statement, "Achilles catches the tortoise" may be assumed true and added as a premiss.
AP10 Achilles catches the tortoise.
And, by the earlier mathematical analysis, this corresponds to assuming the axiom of infinity. The truth of the premiss is demonstrable by means other than the system of premisses and inferences, so we cannot argue that the premiss could be assumed to be false. We are without a means to demonstrate its truth, and that is an epistemological issue. The fallacy is in confusing epistemological and metaphysical issues. We may not infer that, because we can see no way to infer the truth of a statement from certain premisses, the statement is therefore false. But this seems to be what is happening in the Achilles. Of course, this fallacy is being facilitated by equivocation between different senses of 'always' ('never'). This effectively disposes of "the Achilles" as a paradox.
The first form of the Dichotomy suffers from the same fallacy as the Achilles. The computation may be made somewhat simple by presuming that the total distance to be 1 unit. When Achilles has reached the half way point, his distance traveled is 1/2 the total, and the remaining distance is 1/2 the total. Then, when he has reached half the rest of the way, his distance traveled is the original 1/2 plus 1/2 the remaining 1/2, or 1/2 + 1/2·1/2, and the remaining distance is 1/2 the previously remaining 1/2, or 1/2·1/2. We can safely assume that Achilles, being "the fleetest of all Greek warriors"(7), races toward the unreachable point, and construct a table showing his progress after each "race".
Race # Distance traveled Remaining distance. 1 1/2 1/2 2 1/2 +1/2·1/2 1/2·1/2 3 1/2 +1/2·1/2 +1/2·1/2·1/2 1/2·1/2·1/2 4 1/2 +1/2·1/2 +1/2·1/2·1/2 + 1/2·1/2·1/2·1/2 1/2·1/2·1/2·1/2
The distance traveled for each race after N races can be expressed as the series: (1/2)1, (1/2)2, (1/2)3, (1/2)4, . . . , (1/2)N, and the remaining distance can be expressed as: (1/2)N. The fraction Achilles has already covered after N races is just the sum of the first N terms of the above series and may be expressed as
(1/2)I. This sums to 1-(1/2)N. The proper conclusion is "For all natural numbers N, Achilles has a (1/2)N fraction of a unit remaining to run". As in The Achilles, that Achilles has a positive fraction remaining to run for all N does not mean that he has a positive fraction to run for all time.
There is yet another resolution of the paradoxes. The proposed resolution is one that I have found no mention of in any of the writings. The new resolution can be approached with an example from model-theoretic semantics. A model consists of a language, a set of objects, and an interpretation function from the language to the objects, sets of objects, and relations among the objects. It is not necessary to go into the technical structure of models in more detail to present the formal structure of the proposed resolution.
Suppose there are two such models related in a particular way. The two languages are different, and the set of objects from one model is a proper subset of the objects from the other model. For the purposes of this discussion I shall refer to the model whose objects are the proper subset as the limited model; I shall refer to the other one as the general model. I shall also use these terms to refer to the respective parts of the models.
In such a structure it is possible to use a set or sequence of terms from the limited language to pick out an associated set or sequence of limited objects. Since these objects are also members of the objects in the general model, a corresponding sequences of terms in the general language can also be constructed. Because the languages are different, there is nothing to suppose that there cannot be additional objects, in the general model and not in the limited model, which may be selected by the terms of the general sequence.(8) By way of an analogy we may correlate colloquial language with formal language, and reference to the interpretation function. Under this analogy, when a formal language term picks out some object or set of objects, the colloquial language refers to or describes the analogous object.
In the first form of the dichotomy, Achilles' inexorable dash achieves and passes the limit, not by following the sequence as N gets bigger (limited language), but by remaining in motion for a sufficient time (general language). The distance covered is the product of the velocity and the time elapsed. Under my new resolution the first form of the dichotomy and the elapsed time argument are both descriptions of the physical race. It is possible to describe Achilles' position using the infinite series method only up to the limit of that series. The language of the series cannot describe what happens at or beyond its limit. The description of the race using linear velocity, time, and distance can describe what happens at and beyond the limit of the series. Since the infinite series or limited system of representation cannot describe events past its limit, its use should be suspect.
The general fallacy implicit in the arguments seems to be the belief that the totality of all languages can describe everything -- that nothing can exist that language cannot describe -- a point not universally accepted. Colloquial languages can describe things which do not exist, and we are accustomed to describing only those things the language can describe. Like the blind-spot, the contents of which we do not see, and the existence of which we are normally unaware, languages have limits; they do not describe some things, and we are normally unaware that indescribable things may exist. It is quite clear that limited subsets of language cannot describe everything the whole of language can. That a particular subset of language, which we might call a system of description, cannot describe certain objects does not entail that those objects cannot exist. Yet that is just what both the Achilles and the Dichotomy would have us accept.
The second form of the dichotomy suffers from equivocation on the sense of 'complete' as well. The idea that Achilles can't even get started comes from the view that his first step must be onto the "last" member of an infinite sequence of bisections. If the sequence is "complete" in the sense of coming to an end, then Achilles can step onto that end for his first step. But no such end exists, so Achilles has no place to make his first step. This view requires that the members of the series and the starting point stand in the successor relation to each other. But the limit of a sequence does not stand in the successor relation to any of its members. 
0 has no predecessor.(9) [See the discussion at the bottom of page 60.] The limit of the sequence stands in a relation to its members not unlike that of the
relationship of a pedestal to the floor around it. Whenever Achilles steps off the pedestal down onto the series, he has already stepped past an infinite number of elements -- however small his step. Similarly, he cannot get back on the pedestal by following the successive steps; he must jump up through an infinite number of steps onto the pedestal (the first form of The Dichotomy).
With the pedestal analogy in mind, the second form of the Dichotomy seems not to pose a problem as long as extension can continually be divided in half. If it can, then the conclusion seems acceptable. Nothing would be wrong with "covering" an infinite number of points. But the conclusion depends upon the presumption that extension is, in fact, infinitely divisible by bisection. If, at any stage in the process, half way becomes an indivisible minimum, as would be the case were extension not infinitely divisible, then getting half that way becomes an impossible act. In other words, this argument begs the question by presuming that extension is infinitely divisible. It is supposed to prove atomism by concluding that an infinite number of points must be covered -- on the premiss that covering an infinite number of points is an impossible act. But there are an infinite number of points to cover only if extension is infinitely divisible; the argument contains a premiss which presumes the purported result. One cannot cover half the minimum distance. The premiss "for Achilles to reach any point he must get half way" is not true when the point he must reach is only the minimum distance away. He must get there in one fell swoop since there is no intermediate "half-way" point. That he can cover an infinite number of points entails the presumption of divisibility.
J. O. Wisdom noticed the difficulty in "Achilles on a Physical Racecourse", but he interpreted it as supporting his contention that the argument is intended to apply to theoretical divisibility.
This, I think, is the easiest way of seeing that Zeno's premiss cannot characterize a physical race: the 'and so on' is inapplicable because somewhere two neighboring physical points will touch each other and it will be impossible to subdivide the distance between them without altering the assigned size of the points. [sic](10)
James Thomson attempts to resolve the problems of infinite divisibility by appealing to the definition of "infinite" in the sense of arbitrarily large. Any such number chosen is still finite. He distinguished this sense from the sense in which "infinite" is taken to mean an unending process and from the sense in which infinite means the first number which every finite number is less than (0).
[T]o say that a lump is infinitely divisible is just to say that it can be cut into any number of parts. Since there are an infinite number of numbers, we could say: there is an infinite number of numbers of parts into which the lump can be divided. And this is not to say that it can be divided into an infinite number of parts. If something is infinitely divisible, and you are to say into how many parts it shall be divided, you have
Thomson proposes that it is the infinite number of ways that an object may be divided that unpacks what "infinitely divisible" means. In any such way of dividing it, the object would actually be divided into only a finite number of extended parts. This alternative avoids the obviously contradictory notion of completing an unending process of repeated division. This is not, however, the argument Zeno advanced, and Thomson defines the notion of "super-task" for the purpose of resolving Zeno's argument.
Thomson defines a super-task as a task that is completed if and only if an infinite number of tasks are completed. To suggest that an infinitely divisible object is actually divided in this way would be to presume that an unending sequence of divisions had been completed. The presence of both "unending" and "completed" in the reformulation of this premiss makes it rather obviously self-contradictory (if 'complete' is taken to mean 'came to the end').
It is just this apparently self-contradictory nature which determines the actual formulation for the axiom of infinity. In terms of ordinary numbers, the axiom can be stated: there is a number X (infinity) such that 1<X and whenever N<X then N+1<X.(12) By formulating the axiom in this manner, one makes no attempt to "complete" the process of "+1" in any way whatsoever; one merely conforms to the requirements of mathematical induction. We may use induction to infer that for all N, N<X.
Notice that X is not the successor of any number N because N+1<X. There is no number N whose successor is X; consequently, X does not have a predecessor(13). Thomson alludes to this point, but is not explicit at all.
But it is obviously unreasonable to ask where the runner was when he was at the point immediately preceding his destination. [Italics mine](14)
One reason it is unreasonable is that there is no such point; that is,0 has no predecessor.
If the infinite sequence of remaining halves has been traversed and one is at the point 1, this is equivalent to having ascended to the number 0. But 0 has no predecessor so there is no immediately preceding point to have been at. Most people are more familiar with decimal mathematics, so the equivalence may be better illustrated by taking the fraction traversed (in the Dichotomy) to be 9/10ths rather than one half. The first step covers 9/10ths (.9) of the way; 1/10th remains. The second step covers 9/10ths of the remaining 1/10th
(9/10×1/10) or .09, and the total distance traversed after two steps is .9 + .09 = .99. The next step covers .009 for a total of .999. "Completing" the "super-task" mentioned above requires traversing .999999..., and it can be shown that that is just
being at 1.
The following demonstration shows that the number expressed by .999999... is the same number as is expressed by 1. If these are the same number, then to have traversed all the remaining 9/10ths is just to have reached 1.
Completing the sequence of repeatedly getting 9/10ths of the rest of the way just is being at 1. In other words, if one has completed the sequence then one is at 1. So, by modus tollens, if one is not at 1, one cannot have completed the sequence. Consequently, one cannot have completed the sequence without being at 1. To presume that one has completed all the points in the sequence but is not at 1 is to presume a hypothesis that is false -- which leads, of course, to anything at all.
Owen seems aware of this, but violates it in the same breath that he denies doing so.
Notice that Zeno is not first setting up a division which cannot have a last move and then asking, improperly, what the last move would be. He is asking, legitimately, what the total outcome of the division would be; and for there to be such an outcome there must be a smallest part or parts.(15)
The size of the parts is bounded below. In fact, there is a greatest lower bound, and it is zero. However, this greatest lower bound is not in the set of sizes. Consequently, contrary to the above claim, there is no smallest part or parts. Because there is no smallest part we cannot conclude that the size of any such parts resulting from the division process is zero. Mathematical induction shows that it is not. The size of the parts is bounded below by zero, but no part is of size zero, and there is no smallest part. The real numbers under the usual order relation are not "well-ordered". If they were well-ordered, then the greatest lower bound would be in the set, and there would be a smallest (last) member whose size would indeed be zero.
The physics of the relation between position and velocity has some interesting structural consequences. The Heisenberg Uncertainty Principle states that the position and the momentum (velocity) of an object cannot be simultaneously measured to any degree of accuracy; accuracy in the measurement of one is lost at the expense of accuracy in the measurement of the other.(16) A homely macroscopic analogy illustrates this principle.
Take a photograph of an object in motion. The length of time the shutter is open (the reciprocal of the shutter speed) can be used in conjunction with the amount of blur in the image to estimate the speed of the object. The longer the shutter is open the longer the blur and the more accurately the speed can be measured. But the longer the blur is, the less accurately one is able to determine the position of the object. Conversely, the sharper the picture is, the more accurate knowledge of the position of the object will be, but the more uncertain knowledge of its velocity will be.
In Zeno's thought experiment a very sharp view, namely, the arrow being "in its place", is taken; this leaves no blur at all to use in determining the velocity. The mental shutter speed would have to be infinite to obtain an indivisible instant -- we are left with an instant with zero duration. Since motion is measured by determining the ratio of distance traveled to the time duration, Zeno's thought experiment leaves zero (length blur) divided by zero (length duration) for the computation of velocity. And zero divided by zero is undefined. One has perfect information about the position but no information about the velocity. While it is true that a stopped object leaves no blur, it seems fallacious to assume that velocity is zero when one sees no blur. And any blur at all does have the immediate consequence that the object is indeed occupying a space larger than itself.
It has been argued that an object always takes up the space it occupies. It can also be argued that an object in motion always takes up less space than it occupies. Relativity theory holds that an object in motion is contracted in the direction of motion. The shortened length, X', can be calculated in terms of the at-rest length, X, and the velocity, V, using the Lorentz contraction equation. That equation is X'=X(1-V2/C2)1/2, where 'C' is the speed of light.(17) The faster an object is moving, that is, the larger V is, the smaller X' is. If an instant is indivisible and is the same "size" regardless of whether the object is at rest or in motion, then the moving, and hence contracted, object takes up less space; it has room to rattle around in the same sized instant which immobilizes the object at rest. But according to relativity theory objects in motion experience a time dilation effect. That can be interpreted to mean that the size of an instant is increased or "stretched".(18) This gives the moving object even more room. Also according to relativity theory faster moving objects are contracted more. The greater the contraction, the relatively greater the room to move -- and hence the greater the speed possible.
Consider the possibility that an instant is indivisible in the sense that it has no duration. An instant without duration is not consistent with our usual definition of velocity. Velocity is the ratio of distance traversed to the duration in which the traversal occurs. An instant with no duration would be just the temporal coordinate of an object. Taken together with its position coordinate, the result forms the event coordinates of a particular space-time point. It is not possible to determine the velocity of an object on the basis of a single event. At least two events are required. Even our notion of velocity at a point depends upon more than one event. We define the velocity at a point as the instantaneous rate of change of position with respect to time. An instantaneous rate of change, from the differential calculus, involves taking the limit of the ratio of the change in position (distance) to the change in time (duration) between two points. That limit may be some definite quantity, but all computations not at the limit require an extended duration, and no computation is possible at the limit (the denominator would be zero, and division by zero is forbidden). If an instant has no duration, then no velocity within the instant is possible. Velocity at an instant is not determinate without reference to the context of the instant, that is, events external to the instant.
The renditions of the argument as I have presented them significantly reflect our modern view of motion. The Arrow as originally presented speaks only to motion within an instant. The definition of motion I proposed, a modern one, in conjunction with the attending argument concludes, validly, that motion is a phenomenon that is "trans-instantaneous". If instants are infinitely divisible, as the divisionists presume, then any moving object exists in different places (equal to itself) at different instants, as close as you like. On the other hand, If instants are atomic, as the atomists presume, then any moving object exists in different places (equal to itself) at different instants, and the motion is as described more fully in the discussion of "uniform" velocity on page 72 below. But in both cases the concept of moving, as we understand it, cannot apply "within" an instant. Our concept of motion, which is based upon infinite divisibility, requires that we think of objects as moving continuously. If we think of instants as intervals (durations), that means we think of the object as crossing each interval continuously until it enters the next instant, crossing that into its successor, etc. But this view is not consistent with atomism, as the Arrow shows.
The alternative to an instant with no duration is an instant which is indivisible in the sense that it is atomic, that is, that it has a minimum but indivisible duration. It is exactly this premiss that is used in the argument known as The Stadium.
The stadium purports to prove that objects may pass each other without ever being opposite one another. That conclusion is presumed to be absurd and stands as the basis for seeing The Stadium as a paradox. But we seem to have actually observed just such behavior in the context of quantum mechanics, and that observed physical behavior may be offered as an empirically based counter-example to The Stadium. Protons appear to "by-pass" a point where they cannot physically exist in the physical process known as tunneling.(19) A proton in a radioactive nucleus having enough energy to exist outside the nucleus is confined to the nucleus by a potential field with an annular region requiring a greater potential than the energy of that proton. Because the proton has less energy than is required to be in this area, the area is called a potential barrier. This barrier confines the proton to the region of the nucleus of the atom. There is also a region outside the potential barrier in which the potential is less than the proton requires to be there. For a proton to traverse from the inner region to the outer region, it must pass through a region requiring more energy of its occupants than the proton has. The probability of the proton being located there is therefore zero, but the observation is that some protons do get out.(20) They do so without being in the restricted region.(21) They are described as having "tunneled"(22) through the potential barrier.(23) In doing so they, in effect, "march" past others without ever having been opposite them.
Relativity theory offers us another model that is incompatible with our "common sense" experience. Relative velocities do not add according to ordinary arithmetic. The relative velocity of the row of soldiers marching left to the row of soldiers marching right (V3) is not just the sum of the relative velocity of the row of soldiers marching left to the row of soldiers standing (V1) plus the relative velocity of the row of soldiers standing to the row of soldiers marching right (V2). In the case of very high velocities the sum can be nearly the same as the original velocities. The formula for the resulting velocity -- the law of addition of velocity -- in terms of ordinary addition, is:
, where all velocities are expressed as a fraction of the velocity of light (C).(24)
Suppose our soldiers are marching very fast. If the relative velocity of the moving soldiers to the standing ones is nine-tenths the speed of light (.9C) then the relative velocity between the two oppositely marching rows of soldiers is not twice this (.9C + .9C = 1.8C); it is only
.
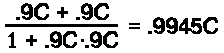In addition, objects moving at relativistic speeds experience a contraction or foreshortening in the direction of travel. This contraction means that the minimum length becomes smaller as the velocity increases. The amount of this foreshortening is computed using the Lorentz contraction formula -- X' = X(1 - ß2)1/2, where ß = V/C.(25) In the case of the soldiers marching at .9C relative to the standing ones, the contraction computes to (1 - .92)1/2 = .4359. This means that two of the moving soldiers take up less space than one standing one -- with room to spare! This would mean that the moving atomic units would take up enough less space that both could be opposite the one stationary atomic unit at the same instant. As the fast moving soldiers pass the standing ones, the minimum distance in the direction of travel has shrunk by over a factor of two to one. This, paradoxically, would allow two moving soldiers to be opposite one standing one! Since this is true of both rows, a standing soldier would see two moving ones on each side, and they would appear to be passing one another.
In the case of the soldiers marching at .9945C relative to the row of oppositely marching soldiers, the contraction computes to (1 - .99452)1/2 = .1050. If one takes a "stand" with one row of moving soldiers, the relative contraction of the other moving soldiers is nearly a factor of 10 to 1. This would allow nearly 10 soldiers to be opposite one! But relativity has its own paradoxes. To the other moving soldiers, it would also seem that ten were opposite one.
There is other evidence that calls into question the argument of the stadium -- evidence that does not need to evoke relativistic speeds. This particular evidence comes from the studies of human perception. As such it represents an epistemological approach. We believe that we can perceive smoothly continuous motion and that that smooth perception would contradict the atomistic assumptions about time and space. However, psychological experiments show that velocity perceived as smooth may in reality not be smooth. In the experiment an observer sees two distinct lights. One is turned off and the other is turned on in sequence. Within a narrow range of the parameters of separation and the duration in which both lights are extinguished, the two lights appear to observers as one light which moves smoothly instead of as two lights which blink off and on respectively. The underlying neurological processes involve the length of time an image of a stimulus is retained in the neural circuits and our experience with moving objects. Under certain conditions we cannot perceptually distinguish between a continuously moving object and one which ceases to exist at one point and then begins to exist at another point (as would be the case under the hypothesis of atomism). An argument from the perception of smooth motion that atomism is false fails because perceptual experiments show that smooth perception arises in response to atomistic jumps in motion.
It seems clear that the various writers recognize that movement involves a change of position over different parts of a span of time. But the two arguments, the arrow and the stadium, seem to presume that motion is somehow continuous. Continuous motion would require continuous space and time. The arguments suggest that a contradiction results from assuming that space and time have an atomic structure. The contradiction actually results from the implicit assumption that movement does not also have an atomic structure. Were movement to also occur in discrete units, no contradiction would arise. A discrete movement would occur when an arrow was in one position at one instant of time and in another position in another instant of time (like electrons changing energy levels in "atoms"). Clearly, the slowest non-zero "uniform" velocity occurs when the arrow occupies the adjacent position during the successive instant. A slower motion would require the object to remain "at rest" in the same position during more than one successive instant. Such motion would be full of starts and stops. However, a faster motion would require "skipping" positions. Moving twice as fast would skip every other position. But it is the assumption that motion is continuous that is required to show that an object must also pass, or be in, any intermediate position. The mean value theorem in calculus proves that, in the case of a continuous, monotonic increasing function, the midpoint must be passed by the function at some intermediate point. A key prerequisite for this theorem is that the function concerned be continuous.(26) It is similarly so with the paradoxes of the arrow and the stadium. For the arrow which moves twice as fast to occupy the intermediate position, it must also occupy an intermediate instant. But by assumption there is no intermediate instant -- because time is assumed to be atomic and not continuous. Motion cannot be continuous when time and space are not. Assuming that motion is continuous assumes a contradictory premiss and anything follows.
If something is composed of parts then the parts must also be composed of parts, ad infinitum. This leaves open the question "what is a part?" To give a definition of "part" in the context of the plurality hypothesis, one must necessarily produce a circular definition. "A part is that which is composed of parts." In modern times we could salvage this circularity by making the definition recursive.(27) "A part is either an ultimate part, or it is composed of parts." Of course, for the definition to be satisfactorily recursive, it must provide some reassurance that parts are composed of ultimate parts after a non-infinite number of reentries. It is, after all, the finite number of reentries that distinguishes recursion from circularity and infinite regress. The plurality hypothesis, as it is represented, entails a circular definition of part just because there is no base case definition of a part nor any way to terminate the regression back to such a base case after a finite number of tries. A part is a part is a part is a part can continue infinitely.
Many of the premisses no longer command the loyalty they once did. There are many counter-examples that cast doubt on the truth of the premisses. I shall examine each statement which forms a part of the argument (as presented on page 41) and present one or more examples where the premiss entailed by the statement no longer holds.
Consider the first statement, "Ultimate parts must have no magnitude or they would not be parts." This statement just defines what an ultimate part is. An ultimate part is just a part with no magnitude. The second statement, "But an extended object cannot be made up of parts with no magnitude", is questionable in the light of modern physical theory. According to the standard model in modern physics, the extended proton is composed of a finite number (3) of unextended quarks. The proton consists of two up and one down quarks.(28)
The proton and neutron are both about 10-13 cm, or about 1/100,000 of the size of an atom. . . . By indirect means the sizes of quarks and electrons are known to be less than 10-16 cm, less than 1/1000 of the size of neutron or proton. Indeed, there is no evidence that these particles have any size at all, they may be thought of as points of matter occupying no space.(29)
This clearly shows that the third statement, "A finite number of unextended parts cannot comprise an extended whole", is not true for particle physics. While, for practical purposes, the premiss is almost always true, it is a fallacy to apply it by analogy to sub-atomic particles.
Modern mathematics also permits questioning this premiss, as Grünbaum notes.
In the context of modern mathematics, Zeno is thus defying us to obtain a result differing from zero upon adding all the lengths of the super-denumerable infinity of points that compose a unit segment. This means that we are being asked to add as many zeros. To Zeno's mind, it was axiomatic (1) that such an addition is necessarily feasible and permissible and (2) that the result of any addition of zeros would be zero, regardless of the cardinality of the set of zeros to be added. But he could not anticipate that the addition of a super-denumerable infinity of numbers, be they zero or positive, presents a problem altogether different from adding either a finite sequence of numbers such as 3, 4, 7 or a denumerable infinity of numbers such as 1, 1/2, 1/4, 1/8, 1/16, 1/32, . . . .(30)
There are two models from mathematics. The easier model is from integral calculus and is the definite integral, which involves denumerable infinity. The definite integral of a function computes the area under the curve between two limit points. Such a function is integrated by dividing the area under the curve into a finite number of pieces, summing the area of the parts, and then by taking the limit of the sum as the number of parts gets larger and the parts themselves get smaller. The limit of the number of the parts is infinite. The limit of the size of each part is zero.
The sum over these parts can be non-zero and non-infinite. For a simple example, I will show the steps involved in integrating the function X2 over the interval from 0 to 1 --
X2dx. While there are many different methods for approximating the area under the curve, the simplest involves treating each segment as a small rectangle. First, the interval is divided into N pieces. The width of each part is 1/N, but the height depends upon which rectangle (the Ith) is considered. Since the function X2 always increases, the right-most point of each rectangle is the highest point in the interval. If we call it the Ith rectangle (out of N of them), that height is (I/N)2. The area of the Ith rectangle is its width times its height: (1/N)(I/N)2. The area under the curve is approximated by adding the area of all these small segments. That
value is just the sum from I=1 to N of (1/N)(I/N)2 -- (1/N)(I/N)2.
Computing the exact value of the area just involves taking the limit as N approaches infinity. Since the size of each piece is (1/N)(I/N)2, this limit is zero; and the limit of N is infinity. We have an infinity of parts of size zero, yet the resulting area is neither zero nor infinite. To show that the sum is a definite number we can algebraically manipulate the sum before we take the limit. The expression for the sum can be simplified by factoring out (1/N). This reduces to (1/N)3(I2). But I2 = N(N+1)(2N+1)/6,(31) so the sum is the product of this and (1/N)3 -- (1/N)3[N(N+1)(2N+1)/6)]. This multiplies out to [(2N3+3N2+N)/6]/N3. Simplifying, we get 1/3 + 1/(2N) + 1/(6N2),
which, as N approaches infinity reduces further to 1/3. So, X2dx =
[1/3 + 1/(2N) + 1/(6N2)] = 1/3, which is clearly neither zero nor infinite.
The second mathematical model involves taking transfinite sums of infinitesimals. These can also be non-zero and non-infinite. Illustrating the model is not necessary, however, as the principle is similar to that of integration.
The statements, "Parts of zero size add up to zero size. So an extended object must be so small as to have no magnitude", commit another fallacy when it comes to the context of an infinitude of parts. Adding the same quantity many times is the same as multiplying that quantity by the number of times it is an addend. For example, 10 added to itself 4 times (10 + 10 + 10 + 10) is 10 multiplied by 4. In the immediate context adding an infinitude of zero sizes, that is, adding zero an infinite number of times, is the same as multiplying 0 times infinity. But multiplying zero times infinity is one of the undefined operations, or at best produces an indeterminate result. That zero times anything is zero is a fallacy; zero times infinity is not defined.
The next statement in the argument is: [Therefore,] "the parts must have magnitude." Ordinarily, the argument to this point would constitute a reductio that there can be ultimate parts or that an extended object can be made up of ultimate parts, but the argument proceeds (rhetorically) for effect.
From "the parts must have magnitude" it does not follow that that magnitude must have a non-zero lower limit. Look, for a moment, at the process of bisecting an extended length. For simplicity take the length of the extended object to be 1 unit. When the first bisection is completed the length of each part is 1/2 (half the length of the original). Now consider a part which results when the unit has been bisected N times. Its length is (1/2)N. (1/2)N is still extended. When we bisect that length the result is also still extended and is of length (1/2)N+1. I have just shown that bisecting (dividing) an extended length yields an extended length for N=1 bisections. I have also shown that whenever the length after N bisections is extended, then so is the length after N+1 bisections. These two premisses satisfy the requirements for mathematical induction and we may conclude that "for all N, after N bisections the length is extended". So, the process of bisection yields an infinity of parts, all of which are extended. But notice that after one bisection there are two parts of size 1/2; after two bisections there are 4 parts of size 1/4; and after N bisections there are 2N parts whose length is (1/2)N. In each case the total length of the parts adds up to the original length.
To assert that an object is composed of unextended parts because this limit of the size of the parts is zero is just not valid reasoning. The flaw is very subtle and has been the basis of controversy in mathematics for millennia. It confuses the limit of a sequence with the members of that sequence, a point which Thomson notices:
Hence Whitehead emphasized that the sequence
was convergent and had a finite sum. He also thereby pointed out a play on the word 'never'; the sequence never reaches 0, the sequence of partial sums never reaches 2. (The sequence does not contain its limit: but it is convergent, the limit exists.)(32)
The argument, "But an infinity of extended parts must have infinite extension", is based upon the unwarranted assumption that because the parts are all extended there must be a smallest non-zero size to the parts. Were there such a limit, then infinite extension would follow. But there being no such limit, infinite extension does not necessarily follow. Some infinite series converge; some diverge.
This argument goes past the point of establishing a contradiction, and hence a reductio; I would think that it does so for the poetic license of being able to say that an object composed of a plurality of parts must be both small and large without limit. The argument above purports to establish the existence of an extended object with no magnitude. It actually establishes that an object made up of parts cannot be made up of ultimate parts. A missing premiss is that any object composed of parts is composed of ultimate parts.
The question that arises is: are ultimate parts composed of parts? The first tendency would be to say no, that that would prevent their having been ultimate. But a second reading is possible. That ultimate parts have no magnitude does not mean that they have no parts. A line has no width but it has both a left and a right side. Moreover, these parts combine to form the whole which has no magnitude (width). An alternate definition of 'ultimate part' could be: "A part is an ultimate part if it has no parts." But this alternate definition clashes with the notion that a part is composed of parts ad infinitum. There can be no ultimate parts under the plurality hypothesis if ultimate parts are parts which have no parts.