Atomism and Infinite Divisibility

ARISTOTLE (384-322 BC) AND INFINITE DIVISIBILITY

Before we can reasonably examine Aristotle's views on the subject, we need to briefly outline the events and conditions that transpired between Zeno and Aristotle. It was during this period that true Atomism was born.

The Birth of Atomism Proper

The birth of atomism in its modern form can be traced to a reinterpretation of Melissos's arguments to support Eleatic monism. Melissos re-presented Parmenides' arguments in Ionic prose, but he deviated from Parmenides' teachings. Parmenides claimed the real was a sphere, which suggests that the real was finite. Melissos claimed that the real was infinite.

The real, he said, could only be limited by empty space, and there is no empty space.⁽¹⁾

Melissos also presented a reductio argument against pluralism.

If there were many things, they would have to be of the same description as I say the One is.⁽²⁾

While Parmenides had earlier advocated the spherical nature of the one, it was Melissos's assertion that there was no empty space that suggests the next development. Combining Parmenides sphere with the denial of both Melissos's assertions, that the real is infinite and that there is no empty space, yields a spherical non-infinite "real" in existing empty space. The denial of monism multiplies these non-infinite reals and produces atoms. That task fell to Leukippos.

It is certain that Aristotle and Theophrastos both regarded [Leukippos] as the real author of the atomic theory.⁽³⁾

Leukippos modified Melissos's statement into the proposition that there are many things and that they are all spherical as Parmenides had said the one is, but not infinite. He also denied the non-existence of empty space. Creating empty space provides a "place" to put these many little "reals". This development can be seen as distinguishing between substance and existence. Prior to this distinction, substance was that which existed and non-substance or void was that which did not exist. When the two notions are distinguished, then it is possible to have non-substance that exists (void).

Prior to Leukippos the strong association of being with anything that could be thought of or said constituted a denial of a void in nature.⁽⁴⁾ Whatever is thought of is, and the world is full of substance. Nothing could not exist and could not be thought. Arguments fairly raged about whether that substance was one or many, and if so, how many. But it was Leukippos who distinguished between non-existence and empty space.

Leukippos supposed himself to have discovered a theory which would avoid this consequence [the impossibility of motion and multiplicity]. Leukippos was the first philosopher to affirm, with a full consciousness of what he was doing, the existence of empty space. The Pythagorean void had been more or less identified with 'air', but the void of Leukippos was really a vacuum.⁽⁵⁾

Taking this new distinction literally poses problems for Aristotle later when he struggles with point and place. (See page 120. below.)

This distinction is also more clearly made when Democritus clarifies and expands Leukippos's theory.

Leucippus had been content to speak of it, as did the Eleatics who denied that it existed at all, as the 'not-real' or 'non-existent' 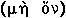: according to Aristotle, Democritus, taking advantage of the distinction between the two Greek negatives, called it the 'unreal' 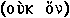or the 'nothing' 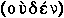. He was in this way able to distinguish the void whose existence he affirmed as stoutly as Leucippus from absolute non-existence 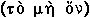, and to dispose of his opponents' objections by phraseology as well as argument. . . . 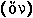'space' was not 'the real' , not body, neither was it the 'not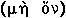-real' , that which does not exist at all, but only 'unreal' 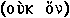. The distinction is a strong reinforcement of what Leucippus meant.⁽⁶⁾

No one, even in modern times, has given a more classic expression to atomism . . . the only differences allowed to the elements are strictly geometrical, plus the motion in space necessary to alter their positions. For Democritus therefore two principles explain everything: atoms and empty space. . . . In the first place, each atom is indivisible. The word atom itself means indivisible; it was for that reason that Democritus invented the term atom and applied it to his elements.⁽⁷⁾

A number of things come together here. Matter and space are distinguished from existence and non-existence. It is denied that matter has both infinite extent and infinite divisibility. But plurality is preserved by limiting its scope. This actually foreshadows the development of recursion in the twentieth century. It also disposes of the problem of infinite regress implicit in the notion of infinite divisibility. We also have each of the types of matter previously conceived preserved as individual types of atoms. This polished atomic theory holds together quite nicely, although its incompatibility with geometry will readily become apparent. We now turn to Aristotle's struggles with this and his rejection of the atomic theory.

Infinite divisibility had already long been a topic of philosophical discussion before The Philosopher came on the scene. Aristotle, in his characteristic way, summarized selected arguments about it in his On Generation and Corruption⁽⁸⁾ and, to a lesser extent, in The Physics.⁽⁹⁾ He accompanied these summaries with critical analyses which include his reasons for rejecting the views of the atomists. Aristotle is not putting forward a positive model of infinite divisibility; he is presenting the horns of the atomists' dilemma and rejecting both horns.

The atomists say that there must be atoms, because things being infinitely divisible leads to the absurd conclusion that there is nothing left to reassemble. Aristotle argues that although things are infinitely divisible, they are not divisible everywhere. He thus rejects a premiss of the atomists' necessary to conclude that nothing is left to reassemble. He does not go further and present a positive account of infinite divisibility.

Here is the abstract form of the atomists' and Aristotle's arguments.

	The Atomists:		Aristotle:
	Either A OR B.		Either A OR (B' AND NOT B).
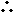	IF NOT B THEN A.		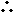IF (B' AND NOT B) THEN NOT A.
	IF B THEN C.		IF X THEN (B' AND NOT B).
	NOT C.		X.
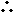	Conclude NOT B.		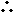Conclude (B' AND NOT B).
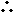	Conclude A.		Conclude NOT A.
A - Reality is made up of atoms.
B - Reality is everywhere divisible.
B' - Reality is anywhere divisible.
C - There is nothing left to reassemble.
X - Point is not contiguous to another point.

 There are flaws in both arguments. In what follows, I shall examine Aristotle's critical analyses and supporting definitions from various perspectives. I shall contrast his writings with our current understanding of mathematical infinity, the real-number line, and model-theoretic semantics. My aim is to show that the use of these perspectives allows us to identify problems with his analyses that are otherwise difficult to uncover and to provide some account for one of his more opaque passages. I shall begin by examining his supplementary definitions.

Only divisible quantities may be considered as candidates for infinite divisibility, and Aristotle defines what a quantity is in The Categories.⁽¹⁰⁾ In 4b20 he divides quantity into discrete and continuous. According to Aristotle, number and language are discrete, and lines, surfaces, bodies, time, and place are all continuous (4b22). Aristotle distinguishes between discrete and continuous in the way their parts interact. The parts of discrete quantities do not have common boundaries; the parts of continuous quantities do. Aristotle is also explicit in stating that nothing else is a quantity:

Only these we have mentioned are called quantities strictly; all the others derivatively; for it is to these we look when we call the others quantities. (5a38)⁽¹¹⁾

Aristotle, in The Metaphysics⁽¹²⁾, strongly suggests that quantities, and only quantities, are divisible.

'Quantum' means that which is divisible into two or more constituent parts of which each is by nature a 'one' and a 'this'. A quantum is a plurality if it is numerable, a magnitude if it is measurable. 'Plurality' means that which is divisible potentially into non-continuous parts, 'magnitude' that which is divisible into continuous parts; (1020a7) . . . for these also are called quanta of a sort and continuous because the things of which these are attributes are divisible. (1020a30)

The foregoing illustrates how Aristotle has identified what are quantities and hence what are divisible. A quantity is something that is divisible; on the other hand, anything that is divisible is a quantity. As a result, the phrase 'divisible quantity' is redundant; however, it will often be useful to keep this redundancy in mind. Aristotle has, in effect, established that infinite divisibility can be analyzed only as "infinitely divisible quantity".

The nature of infinite divisibility depends upon the nature of the infinite. To examine the role the infinite plays in infinite divisibility, we must turn to Aristotle's discussion of the nature of the infinite in The Physics. In 202b30 - 203b14, he surveys the opinions of his predecessors concerning the nature of the infinite and includes in the survey opinions of those who affirm infinite divisibility as well as opinions of atomists who deny it.

Some of Aristotle's predecessors held the view that infinity was some real thing itself, a view which Aristotle objects to. In spite of the reification of infinity suggested by his own use of the definite article in his discussions of "the infinite", Aristotle essentially settles on a definition of 'infinite' which rejects its being a proper subject. "Infinite", in his view, is predicated of other things -- magnitude and number in particular as well as time and motion. Aristotle said:

Some of these do not treat infinity as an attribute of something else but make the infinite itself a substance; but of these the Pythagoreans treat it as present in sensible things, and also describe what is outside the heavens as infinite, while Plato recognizes nothing outside the heavens, but makes the infinite a constituent both of sensible things and of ideas. (203a4)

Aristotle rejects these views in favor of a more process-oriented view, one which spans the distinction between atomism and its opposition. He cites supporters of this view from both the atomist camp and their opposition, those who favor infinite divisibility:

Those who make them infinite in number, as Anaxagoras and Democritus do, describe the infinite as continuous by contact. (203a20)

Aristotle supports the rejection of a reified infinity by arguing that the infinite is a principle.

[The infinite's] being ungenerated and imperishable points to its being a principle; for there is a limit to all generation and destruction. This is why the infinite has no beginning but is itself thought to be the beginning of all other things . . . . (203b7)

This argument can be interpreted as follows: If the infinite were a thing then it would be something that could come to be and cease to be. The infinite cannot come to be nor cease to be. Since it cannot come to be nor cease to be, it must not be a thing.

In 203b15-24, Aristotle offers the following as supporting the existence of the infinite.

Belief in the infinite is derived from five sources: (1) from the infinity of time, (2) from the divisibility of magnitudes, (3) from the fact that the perpetuity of generation and destruction can be maintained only if there is an infinite source to draw upon, (4) from the fact that the limited is always limited by something else; but above all, the infinity of number, of magnitudes, and of what is outside the heavens is inferred from (5) the fact that there is no limit to our power of thinking of them; (203b15)

Aristotle's statements of these beliefs seem somewhat question-begging or circular, but they all hint at something which can be continued again and again (presumably without end). He clearly favors the perspective on infinity which treats infinite as an attribute of a process which cannot be gone through. He would certainly agree that the infinite is not a thing which can come to be and cease to be; infinite is that attribute which identifies a process as having no end. Aristotle explicitly gives four senses of 'infinite', three of which include the notion of a process which cannot be completed.

We must first distinguish the senses of 'infinite': (1) That whose nature forbids its being traversed, (2) that which admits of incomplete or (3) difficult traversal, or (4) which, though of such a nature as to be traversable, yet does not admit of it. Again what is infinite is so in respect of addition, of division, or of both. (204a2)

Even though Aristotle's language treats "infinite" as an object, these three senses clearly emphasize the interminable nature of processes that are said to be infinite. That such a process is said to be infinite makes it a "thing" which 'the infinite' is predicated of. In his continuing discussion, Aristotle becomes more explicit in this regard by stating:

For infinity is an attribute of number and magnitude, and an attribute of an attribute is even less capable of independent existence than an attribute. (204a15)

Of course, attributes are predicated of other things. (Infinite is an attribute predicated of divisibility and divisibility is an attribute predicated of magnitude.) Once the infinite is predicated of processes, and limited to the process of addition and division at that, the subjects of the processes come under examination.

Aristotle claims that a thing is infinite only by addition or by division. This is more precisely stated by saying that a thing is infinite only by the process of addition or division. Extracting the essence of this in regard to the infinite yields "the process is infinite". "Infinite" is then predicated of a subject. The only subjects he deems appropriate are magnitude, number, time, and motion. In regard to addition, Aristotle concludes, "Clearly then there is no actually existent infinite body" (206a7), a conclusion with which modern science agrees.⁽¹³⁾ He goes on to apply divisibility to extension.

Spatial extension is not infinite in actuality, but is so (a) by division (the belief in indivisible lines is easily refuted); (206a17)

So, the infinite is not actually predicated of magnitude per se. It is the divisibility of magnitude -- the process of dividing -- that infinite is actually predicated of.

Aristotle's discussion of infinite divisibility in The Physics is intended mostly to elucidate "the infinite" rather than to address the topic of infinite divisibility itself. The parenthetical insert at 206a17 is not justified. It appears to be question-begging. Suppose the atomists were right. First consider the simple case of dividing a line by the process of bisection. If each line were always divisible exactly in half, it would have had to have had an even number of points. Not only would the number of points have to be even, it would have to be an exact power of two -- 2, 4, 8, 16, 32, . The consequence would be for lines of four and eight points to exist but not for lines of six points. Bisecting a line of length six yields two lines of length three -- a length not capable of being bisected. This is clearly absurd (except, perhaps, to the Pythagoreans).⁽¹⁴⁾ The alternative would be for a line to have had an unending supply of points. But having an unending supply of points is just having an unending supply of places where it is divisible. Therefore, to presume that a line is divisible exactly in half is to presume that it is infinitely divisible. Rather than refuting atomism, this begs the question by assuming infinite divisibility.

Let's examine a bit further the consequences of the atomists' position. Under their presumption, lines will be composed of a finite number of (indivisible and extended) points. To presume that a line may be divisible into two (not necessarily equal) parts is to presume that the line is at least as long as the magnitude of two (adjacent) points. Since a line must consist of at least two points by definition, a line is always divisible into two parts. But the two parts may be single (extended and indivisible) points and hence not proper lines. We can call such a part a degenerate or improper "line". These improper lines are not themselves divisible; hence there is a limit to divisibility (under the presumed atomic structure). Consequently, that there are no indivisible lines, per se, does not necessitate that lines are infinitely divisible. The atomists' position is not as fragile as Aristotle would have us believe; he believes lines are continuous, and his belief has infected his reasoning. His parenthetical remark at 206a17 is gratuitous. It reminds one of the remark Fermat scribbled in the margin of a book -- the remark about the existence of an alleged "elegant and simple" proof of his famous last theorem (which was proven in 1993, but the proof was not trivial).

In The Physics, Book III, Chapter 7, Aristotle asserts a reciprocal relationship between number and magnitude. Number is potentially infinite by addition just as magnitude is potentially infinite by division. Number has a minimum unit while magnitude has an (unspecified) maximum. He concludes:

(1) Magnitude is infinitely divisible.
(2) Number is infinitely addable.

Peano's successor axiom makes (2) explicit with regard to number. "Every number has a successor" captures the notion that number has the nature of being, as Aristotle would say, "infinite by addition"; addition is a never-ending process. Consequently, I cannot argue with (2).

But, it seems to me, (1) can be questioned. Hume and Berkeley both argue against it.

I have approached Aristotle's treatment of "infinite divisibility" by looking first at the logically prior treatments of (divisible) "quantity" in The Categories and "the infinite" in The Physics. Aristotle deals specifically with "infinite divisibility" in On Generation and Corruption. In chapter two of that work he attempts to clarify what 'infinite divisibility' means. He needs to clarify the meaning of 'infinite divisibility', because, as he sees it, several important notions (coming to be, alteration, growth, and undergoing the contrary of these) all depend upon how infinite divisibility is characterized.

Basic to all this is the question whether the things there are come to be and alter and grow and undergo the contrary of these things because the primary existences are things which have size, and are indivisible, or whether nothing which has size is indivisible; this makes a great deal of difference. (315b24)

On a first reading of this chapter, one might think that Aristotle had two models which were not compatible and that their incompatibility could be accounted for by Georg Cantor's account of transfinite numbers. That is, Aristotle could have devised a coherent characterization of "infinite divisibility" had he known of the different orders of infinity as characterized by Cantor.⁽¹⁵⁾ Aristotle was getting apparently contradictory views by tacitly assuming (falsely) that there is only one kind of infinity.

As a result of Cantor's work, we differentiate among infinities of different cardinality (size). The first such division is between the size of the natural numbers and the real numbers, and lines are usually modeled by real numbers. Some of Aristotle's descriptions conform to a cardinality characteristic of the natural numbers and some to a cardinality characteristic of the real-number line.

On a more careful analysis of Aristotle's passages on infinite divisibility, and in consideration of the types of language he uses in describing his analysis, a more subtle reading is possible. The need for different infinities may be too strong. A lesser difference may be sufficient to account for the problem. The difference here is the distinction between so-called "discrete" sets and "dense" sets.

In this particular use of 'discrete', the members of such a set can be placed "next" to each other and be counted. Two elements can be said to be next to each other, successive, or adjacent, if there are no other elements between them. Aristotle's corresponding definitions can be found in The Physics. He defines 'in succession' and 'between' in book 5, chapter 3, in the context of a discussion of motion. For our purposes here, only certain aspects of these definitions are necessary.

'Between' involves at least three terms; (226b26)

That is 'in succession' which, being after . . . has nothing of the same kind between it and what it is in succession to. (226b34)

The natural numbers, with the successor function, is the primary exemplar of such a set and represents the discrete model. In the case of any set of macroscopic objects which are stacked or lined up and can be counted, the "successor" or "next" relation can be shown of any given one of such objects (except the last one in a finite set).

Sets which are "dense" have the property that between any two members of the set another can be found. The real numbers provide the most common example. If you have two real numbers x and y, then the number (x+y)/2 is between x and y.

One's first reaction to Aristotle's problem with infinite divisibility might be to consider the difference between the natural numbers with their successor property and the real numbers with their dense property as providing a way of explaining Aristotle's difficulty. These two sets represent different orders of infinity, so one might be tempted to think the different orders of infinity are required to extricate Aristotle from his difficulties.

In the problem of infinite divisibility, it is the dense property of the real numbers which suggests a difference sufficient to distinguish between the two models. It is not the greater cardinality of the real numbers which is significant, merely their denseness. Another dense set is the set of rational numbers. If you have rational numbers a/b and c/d, then the number (a/b+c/d)/2, which is just the rational number (ad+bc)/2bd, is between a/b and c/d. Just as with the real numbers, between any two rational numbers is a third. But rational numbers have the same cardinality as the natural numbers. The distinction between the dense and discrete property may be adequate to explain the difficulty with infinite divisibility.

One potential source of difficulty is that Aristotle views magnitude as a continuous quantity. "The 'continuous'", says Aristotle, "is a species of the contiguous; two things are continuous when the limits of each become identical and are held together." (227a7) He had previously proposed a definition for 'contiguous' in 227a6: "That is 'contiguous' which, being in succession, is also in contact."

The rational numbers do not form a continuous set. In fact, the set of rational numbers is discontinuous "everywhere" because there are irrational numbers arbitrarily close to any rational number. There are infinitely many irrational "holes" in the (rational) number line. Aristotle's definition of 'continuous' might seem to require a greater infinity than the countable. ('Countably infinite' means having the same cardinality as the natural numbers.) Even the real-number line seems to fail to satisfy his definition of 'continuous'. Two things are continuous if they are of the same kind, are contiguous, and touch. Certain sets of real numbers -- intervals -- can touch and, when touching, form a unity. But two (distinct) single real numbers cannot touch any more than two rational numbers can.

If we ignore the irrational "holes" in the number line, then sets of rational numbers behave just like real numbers as above. In other words, relative to the set of rational numbers, closed interval sets of rational numbers can form contiguous, touching, consecutive sets of the same kind. (They "touch" provided their terminus is a rational number and not an irrational one. For example, the closed interval ending with 2 touches the closed interval beginning with 2. But the open interval terminated by € does not touch the open interval beginning at €since is irrational.) So, some closed interval sets of rational numbers are continuous qua the rationals. Half-open intervals would seem to qualify, but they do not touch, even though there is nothing between them.

The potential/actual distinction applied to divisibility seems to correlate with these two models. That which is potentially divided forms contiguous parts with a common boundary wherever it might be actually divided. The actually infinitely divided would give an exploded view with adjacent parts "next" to one another (but not touching -- as in discrete sets). These views are irreconcilable in that the potentially divided retains its dense structure, while the actually divided does not. Now, we can find a mapping from the natural numbers to the rational numbers showing that there is still the "same number" of points. But the order required by "next" gets changed around.

In 316a16-25, as Aristotle summarizes the Atomists' argument, he is clearly using a dense model when he argues that no body or thing possessed of size is left, since, if anything left had size, it would also be divisible. Such a body has the same structure as denseness in that a point exists between any two distinct points.

In 316a26-33 he is discussing the characteristics of "sizeless" points. Since points have no size, when two of them are placed together they become coincident; that is, only one point remains. Moreover, an object composed of only two points, when divided, still retains the same overall size (two points of no size still adds up to no size). However, generalizing from combining any finite number of points to combining infinitely many points is not valid. But this is just what Aristotle does. He asserts that an object assembled from ("infinitely") many sizeless points cannot have size:

So even if all the points are put together they will not produce size. (316a34)

One suspects that Aristotle doesn't have it all together in view of his previous statement:

Similarly, if it is formed out of points it will not have quantity; for when the points were in contact and there was just one thing possessed of size and they were together, they did not make the whole the slightest bit larger; (316a28)

Aristotle is a bit loose here. Points cannot be in contact without being coincident. In his notes, Williams seems aware of the errors -- he adds quotes to 'in contact' and 'together' -- but he focuses on the issue of continuity and questions Aristotle's mastery of the argument involving the "sawdust model".⁽¹⁶⁾ Joachim notes a grammatical shift of subject at the same point (or is it "place"?)⁽¹⁷⁾

It seems clear to me that Aristotle's mental model involves "exploding" a body of size into discretely separated sizeless parts (points) and then sequentially putting together points two at a time. He is left with only one point after each step. This process can continue for a countably infinite number of steps and still yield the same result: an object the size of one point -- "a set of measure zero".

Something is intuitively wrong when the reassembled parts do not make up the original whole. The flaw is in presuming that "exploding" the original yields discrete consecutive points, that is, gives the same result as a completed infinite division. Mentally explode something slowly; it stretches rather than breaks. The dense nature of a continuous object supplies "as many more points as necessary" to fill in any gaps where it might be [is potentially] divided. Mathematically, an interval of any size can be transformed into one of any other size, including between the finite and the infinite. I will return to this subject later; for now, it is sufficient to comment on the difference between the discrete "exploded view" and the dense "assembled view".

This difference corresponds to the distinction between counting and measuring, about which Ackrill, in his comments on The Categories, says:

Aristotle does not stop to examine carefully the nature of counting and measuring, nor does he survey the different ways in which quantity or quantities may be spoken of; . . .⁽¹⁸⁾

If 'quantity' represents an abstraction subsuming both counted quantities and measured quantities and these are somewhat conflated, as Ackrill implicitly suggests, then Aristotle's apparent shift between a discrete and a dense model is understandable.

There is a problem with Aristotle's use of 'all' when he refers to putting "all" the points together. 'All', in this sense, stands for an undistinguished infinity. By adding all the points together, we have the sum over infinity of a zero-sized body. Summing the same thing many times amounts to multiplying by the number of times; for example, adding 4 a total of 10 times is the same as multiplying 4 times 10. The net result is that adding all the points has the structure of multiplying zero times infinity; that product is mathematically indeterminate.

If we coordinate the division process with the summing process, we can overcome this indeterminate result. Suppose we divide a body into N pieces, each of size L/N where L stands for the length or size of the object. (Remember, Aristotle's conception of the infinite is of a process which cannot be gone through. Dividing a magnitude in an attempt to achieve infinite divisibility by such a process is dividing it with an ever-increasing number of divisions and cannot actually be completed.) Something is infinitely divisible if N is getting larger and larger. Conversely, L/N is getting smaller and smaller, until finally (if there can be a finally), N reaches infinity and L/N reaches zero size. Of course, according to Aristotle, the infinite cannot be gone through; the limit cannot be reached by any direct method. Since the infinite cannot be gone through, any attempt to put things back together must be done with the incompletely divided fragments -- which are of size L/N.

By coordinating the summing with the division, we perform the multiplication of size L/N times the number of segments N and obtain a product of (L/N)·N. Notice that this simplifies to L, and it no longer matters how big N is. So, if we take the limit as N approaches infinity of (L/N)·N, we end up with L, the same size we started with. Aristotle and the atomists neglect the fact that infinity cannot be gone through when they presume something to be infinitely divided. Additionally, both the atomists and Aristotle implicitly presume that infinity times zero is zero. Of course there would be nothing reassembled if this were true. But infinity times zero is not zero; it is indeterminate. The atomists' premiss, that there would be nothing reassemblable, is not compelling. The reductio argument fails.

The atomists' argument is flawed in another way, as is Aristotle's presentation. Here is a greatly expanded version of the argument.

1. Every perceptible body is potentially divisible at every point.

2. It is impossible that a body is actually divisible at every point (simultaneously). (Premiss 2 is proven by reductio in conjunction with premiss 3.)

3. Nothing can come to be out of nothing or cease to be into nothing. (319a16-21)

2.1. It is possible that a perceptible body is actually divided at any point. (Assume the contrary of 2.)

2.2. If a body is actually divided at every point, then there will be nothing left. (Premiss 2.2 is itself proven by reductio.)

2.2.1. If there were something left, it could be further divided at some point, contradicting its having actually been divided at every point.

2.3. If nothing is left, then the body will have vanished into something incorporeal.

2.4. If a body vanishes into something incorporeal, then it ceases to be (something corporeal).

2.5. If something can cease to be something corporeal, then it can also come to be something corporeal (out of points or out of nothing at all).

Therefore, 2.1 leads to the contrary of 3 and absurdity; 2 is proven by reductio.

If a body is not actually (simultaneously) divisible at every point, then consider whether it is potentially (non-simultaneously) divisible at every point.

4.1. If a corporeal body is divided, it is divided into corporeal bodies. (A trivial case is division into a corporeal body and separate points. The corporeal body is not diminished by this form of division.)

4.2. Division into parts cannot yield a process which goes on to infinity because infinity cannot be gone through. Non-simultaneous division is a process of successive divisions which, by the nature of the infinite, cannot be completed. Any stopping point would yield, by 4.1, undivided corporeal bodies.

So, a body cannot be divisible everywhere because either the process could not be completed and something of size would be left, or nothing at all would be left.

The Atomists are happy with the first horn but must further reject the second horn. That rejection flows as follows:

5. If the process were to be carried out to infinity (or simultaneously), the parts would all be nothing at all or vanishingly small points.

6. If coming to be and ceasing to be are to take place by aggregation and segregation, then aggregation must be capable of adding to the size of what comes to be; conversely, segregation must diminish the size of what ceases to be.

7. Aggregation cannot proceed by the accumulation of nothing at all or points (vanishingly small pieces). Conversely, segregation cannot proceed by diminution from vanishingly small pieces or points.

8. Coming to be takes place by aggregation; ceasing to be takes place by segregation.

9. Aggregation must proceed by the addition of pieces of some determinate size. Conversely it is so with segregation.

Here the atomists' argument actually makes a wild leap of faith.

That aggregation must proceed by the addition of pieces of some determinate size begs the question if "determinate" is taken to mean "minimum". The argument is that aggregation must occur by the addition of something of size. Nothing is actually presented to rule out continuous accretion. If there were some non-question-begging way to rule out continuous accretion, we would have a nice, tight reductio. But it leaks.

Aristotle has it that aggregation occurs by "leaps and bounds", that is by the addition of large clumps of material at each "step". These clumps are themselves infinitely divisible but not divisible at every point. He rejects the atomists' solution, retains infinite divisibility, but rejects the notion that objects of size are everywhere divisible. (The real-number line satisfies this by having a countably infinite number of rational "division points" and many irrational "non-division points" but does so by including different orders of infinity.) Of course, Aristotle believes that time is infinitely divisible; there is no problem with half as big an increase occurring in half the time. Continuous accretion is the natural consequence of this model. However, aggregation by atoms goes along equally well with a limit to divisibility of both magnitude and duration. The nature of time (continuous or discrete) would seem to fit in the appropriate model. Even if duration were not infinitely divisible, aggregation could still occur by the addition of divisible clumps at each interval.

Aristotle, however, does not proceed along this line; he takes another tack.

In 316b6 Aristotle introduces a statement from another level of analysis. He states:

And any one contact always involves two things, since there has to be something else besides the contact or division point.

Aristotle asserts that any one contact requires two things, in the sense of distinct things. This requirement seems to be based upon a syntactic-level notion for the word 'contact'. Contact requires two distinct objects touching or "contacting" at a single point. Remaining distinct while still sharing a point (of contact), in truth, requires a minimum of 3 points. Since there is no reason to prefer one object over another, each must provide a point distinct from the point of contact. Otherwise, one object would not be distinct from the point of contact, which is part of the other object as well. We would, in such a case, have one object with a point of contact and no other object. Aristotle's argument is a little weak here, since he asserts only the need for 2 points instead of 3.

His mistake is understandable in the light of the tension between incompatible models: discrete quantities do not have a point of contact; continuous quantities "join" at a point (of contact). Since two distinct discrete quantities do not share a point of contact, no third "point of contact" is required.

This kind of characterization of contact has as a prime paradigm such things as stacks of coins or columns of bricks. Macroscopic objects all have at least two distinct points (and all points between) so can remain distinct apart from a shared "point of contact". Further, the type of such a set of objects is discrete. One can use the point of contact along with the other two distinct points (one for each of the two objects) to evoke the adjacent, or next, relationship. Starting with the point not of contact in object "A" (and we are guaranteed that at least one such point exists), move first to the point of contact and then to the point not of contact in object "B" (and we are guaranteed that at least one of these points exists also). By this method we move from one object to "the next" (a notion Aristotle uses). In doing this, we have ignored any points of objects "A" & "B" except for one point not of contact from each object and the point of contact.

For parts to form a continuous whole, there must be a point of contact between one part and "the next". If something were divisible everywhere, the parts would be mere points -- which, according to Aristotle, cannot be recombined into anything of size. Aristotle must find a way to disallow divisibility everywhere while still permitting infinite divisibility. Lear, in "Aristotelian Infinity", notes:

Aristotle offers a paradigmatically Aristotelian solution. He distinguishes two senses in which a line may be said to be divisible 'through and through' (317a3ff). A length is divisible through and through in the sense that it could be divided anywhere along its length. But it is not divisible through and through in the sense that it could (even potentially) be divided everywhere along the length. One can thus actualize any point but one cannot actualize every point; for any process of division, there must be divisions which could have been made which in fact were not made.⁽¹⁹⁾

Lear, who is more interested in infinity than infinite divisibility, takes the potential/actual distinction at face value and does not elaborate further.

In 317a3 Aristotle states:

Since no point is contiguous to another point, there is one sense in which divisibility at every point belongs to things of size and another in which it does not.

The distinction between these senses will be clear when we examine his argument in the next few lines. It follows from an apparent distinction between his usages of "anywhere" and "everywhere". He goes on to state:

When this is asserted, it is thought that there is a point both anywhere and everywhere, so that the magnitude has necessarily to be divided up into nothing; . . . (317a5)

Here Aristotle begins to hint at his argument by implying a distinction between (divisibility) "anywhere" (hopoun) and "everywhere" (pant) and by using the conjunction "both . . . and" (kai . . . kai) to join them. The rest of the sentence,

for because there is a point everywhere, it is formed either out of contacts or out of points (317a6),

introduces his distinction between places where the line is divisible (contacts) and places where it is not (points).

Aristotle continues with his analysis and refutation of the atomists' argument. He is quite terse in his dealings with it, and the brevity of his rebuttal leaves much to be desired. Williams comments:

The above paraphrase of 317a2-12 is the nearest I can come to making sense of this baffling passage. A large part of it, 317a8-12, is so resistant to my attempts to understand it that I have contented myself with a literal translation which I have placed between obeli to indicate that no claim is made to have found a sure way of making sense of the Greek. Other commentators and translators seem to have fared no better, and I can hope to surpass them only in frankness.⁽²⁰⁾

Better sense, I think, can be made of Aristotle's discussion by fleshing out certain contextual presumptions.

When this is asserted, it is thought that there is a point [where something with magnitude is] both [divisible] anywhere and [divisible] everywhere, . . . . (317a5)

Aristotle is leading to the conclusion that something with magnitude is divisible anywhere but is not divisible everywhere, and since it is not divisible everywhere the atomists' argument is defeated. This distinction can be interpreted as corresponding to the distinction between being potentially divided and being actually divided. Aristotle seems actually to agree with the atomists, though he potentially does not. Although he agrees that there is a sense in which something with magnitude is not everywhere divisible, he denies that it follows from this that magnitude is not infinitely divisible.

Aristotle seems to connect 'anywhere' with "potentially divisible" in the following passage:

In one sense there is a point everywhere, because there is one anywhere and all are like each one; . . . (317a8)

Here, the distinction between 'anywhere' and 'everywhere' is used in an entailment manner: "If there is a point 'anywhere' then there is a point 'everywhere'", with the reason given that "all are like each one". By this Aristotle means that there is no reason to suppose that one point is any different from any other. Potentially, there is a point anywhere.

He goes on with his crucial "point" that "but there is no more than one." By this he means that there is no more than one point anywhere (at each position). His argument to support this immediately follows: "since they are not consecutive, . . .". (317a9)

One might expect 'contiguous' in place of 'consecutive' above. 'Contiguous' would seem to fit more easily in the reading that follows. His use of 'consecutive' at this point seems more in keeping with the undivided, or potentially divided, state under consideration. The undivided line is continuous, so any parts are contiguous to each other; in this state, the parts are not discretely separated by actual division. Consequently, there is no "next" part adjacent to any chosen one. So, two points (parts) are not consecutive. (But they are not contiguous either -- the "parts" of something continuous are normally contiguous, but points are an exception.) Aristotle concludes:

so it is not the case that there is a point everywhere. (317a9)

Sense can be made of the argument at this point if we interpret Aristotle to be thinking of both point and place but ambiguously using the term 'point' for both. We need to recall that, for Aristotle, a point must be actualized in some way. He would say that the place of a potential point does not hold an actual point. We can distinguish between a place where there is an actualized point and a place where there is no (actualized) point (there would be a potential point in such a place). By the symmetry of arbitrariness, any place could have a point. Once such a place is chosen, then the contiguous places have no points. To show how this works, here is an expanded interpretation of the argument at (317a9)

If there were points everywhere, then there would be contiguous points at every point. Contiguous points must touch. Since points take up no space at all, touching points would be in the same place. This would necessitate there being two contiguous points at every place. But there can't be two points at the same place. Consequently, points cannot be contiguous. Since points cannot be contiguous, the "place" of the potential contiguous point must be empty. So, there is a sense in which there is not a point everywhere.

This argument entails a presumption that "place" is both contiguous and consecutive. Every place has both a contiguous place and a consecutive place. So, since points can't be contiguous, there must be places where points aren't, namely the contiguous places.

This is the sense in which there isn't a point everywhere, while the sense in which there is a point anywhere is its potentially having been chosen as the starting "point". I think this establishes that Aristotle differs in his interpretation of (divisible) 'anywhere' and 'everywhere'. He has concluded that even though there is a point "anywhere" there is not a point "everywhere". There is a loose association between the term 'anywhere' and the potentially chosen starting point and the term 'everywhere' and the contiguous places which might hold points -- loose, but not consistent.

There is a kind of logic in his argument which is illustrated by the following example. Suppose we want to talk about "the Universe" and intend by that term to include all things, including all space and all time. Then, suppose someone wants to use the term 'edge', or 'boundary', in talking about the universe as we have defined it. By 'edge', or 'boundary', we usually mean a distinction or division between two things, one of which belongs to one side and the other of which belongs to the other side of the distinction.

"Edge of the universe" presupposes that there is something which is in the universe and, on the other side of the edge, something which is not in the universe. But we defined 'universe' as including all things, so we can conclude that there is no edge to the universe. That is, we cannot consistently use the term 'edge', or 'boundary', with its usual meaning, if we hold the meaning of 'universe', as we have defined it, to include all things. It requires careful analysis to notice that simply using the term 'edge', or 'boundary', with 'universe' introduces a contradiction and yields a (verbal) structure which is no longer consistent.

Aristotle seems to be displaying a similar type of argument, but one which is more subtle, in creating a distinction between the intended usages of the terms 'everywhere' and 'anywhere'. He allows for two senses of 'everywhere', in one of which there is a point (and hence divisibility there) and in the other of which there is not a point (and hence no divisibility there). The argument is confused because he does not create a separate term for each usage and, moreover, does not seem to be consistent in his usages of 'everywhere' and 'anywhere' in regard to the distinguished senses.

In the sentence that follows, Aristotle is referring to the "place" which is contiguous to any point:

For if it is divisible at the middle it will also be divisible at a contiguous point. (317a10)

This appears to introduce a terse reductio supporting his previous sentence.

1. Suppose we have two points (anywhere) at which magnitude is divisible. (He seems to be presuming that he is considering two "consecutive" divisible points.)

2. Suppose it is divisible at the middle (between these two points).

2.1 Then it would also be divisible at a contiguous point. (Either could have been actualized.)

2.2 But it cannot be divisible at both the middle and a contiguous point because there is no contiguous point.

"For position is not contiguous to position or point to point." (317a12)

(Actualizing one precludes actualizing the other, but by symmetry either both must be actualizable or neither can be. And we have shown that one cannot be, so neither can be actualized.)

3. Therefore, by reductio, it could not have been divisible at the middle.

The presumption that any place has both a contiguous place and a consecutive place allows one to conclude that there is a "point" contiguous to the middle point. But points cannot be contiguous (without being coincident).

This presumption allows us to confuse the notions of discrete sets and dense sets, notions which are otherwise incompatible. With our visual model of the real line we think of a continuous set as something in which no amount of "stretching" will create breaks or "holes". Of course, with the rational numbers, which could be thought of as having a "granular" quality, stretching does not separate the grains any more than before stretching. There are always more points between any two points, no matter how close they were to start with.

The presumption that any place has both a consecutive place and a contiguous place cannot be modeled, because it is inconsistent in the context of Aristotle's definitions of 'contiguous' and 'consecutive'. As such, it represents a "syntactic-level" constraint or connection between the two incompatible models.

Aristotle abandons his visual model in favor of this syntactic-level argument when he nonchalantly states "since they are not consecutive". (317a9) He thereby justifies his statement that there is no more than one point anywhere. What he seems to be doing is shifting levels of argument from semantic considerations of the visual model of the real line to more purely syntactic-level constraints. In the semantic-level analysis, which is driven by the visual model, statements are judged by their agreement with the model -- in this case the visual image of the real line. By appealing to the assertion that the points are not contiguous (presumably after division), he allows a shift to the discrete model which provides the appearance of solving the problem. By not consistently sticking to semantic-level considerations, or conversely to syntactic-level constraints, he permits a kind of inconsistency to invade his argument. This inconsistency results directly from the notion that any place has both a contiguous place and a consecutive place.

Aristotle notes that, once an object is divided (into points), no point has a contiguous neighbor; allowing that leads to a contradiction of the hypothesis that the object was divided at every point. He denies that points are contiguous but implicitly assumes that there is a next point, distinct from the "one anywhere", and that the intervening distance is not divisible. He concludes that there are no points in this interval.

His argument here is based upon a view of the divided object represented by an exploded set of separated points, presumably in an array similar to what we see when we look at a newsprint photo with a magnifying glass. This kind of view represents a discrete set of points, while the set of points in an undivided region of space (line segment, or disk in the plane) is a dense set. Aristotle has unwittingly converted from dense to discrete in the middle of his argument.

The remainder of his sentence, "and this is division or composition." (317a12) simply states that he has dealt with the problem of infinite divisibility and, its converse, composition.

In 317a15-18, Aristotle confirms this interpretation when he states:

nor in such a way that division can occur everywhere (for this is what would happen if point were contiguous to point) . . . .

In 317a18, he states:

but into smaller and yet smaller parts, and aggregation out of smaller <into greater>.

Here, he recalls his purpose in examining infinite divisibility, namely to shape the concepts of aggregation and segregation, which will relate to alteration and growth.

Aristotle does not carry the smaller and smaller to its logical limit because he has just argued that there is a sense in which divisibility at every point is not applicable to objects of size. The process of dividing something into smaller and smaller parts seems a simple concept to grasp and, aside from practical considerations, easy enough to carry out, but Aristotle has asserted that there are some places at which the division cannot occur -- those places where there isn't a point. He does not relate the sense in which "there is not a point everywhere" (317a9) to the process of consecutive division.

I would like to have the consequence that there is not a point everywhere directly related to the process, so I could have some model or definition of how the process misses these points. The consequence itself doesn't seem likely. It could be argued that any process which yields any potential division point, finite or otherwise, will always select the point which is "anywhere", making other points the "not-everywhere" ones. In other words, it doesn't matter which points you choose; you can't choose any of the ones at which the thing is not divisible. Non-divisible points are forever inaccessible. Aristotle would say that that's because there aren't any "points" at these places.

Aristotle does not connect the two distinct adjacency criteria in the notion of "place", as instantiated in the two incompatible models (discrete and continuous), and consequently fails to notice the resulting contradiction. Since his purpose was not to clarify infinite divisibility itself but only to clarify it in relation to its use in accounting for coming to be, alteration, growth, and undergoing the contrary of these, he stopped short of unearthing the contradiction.

Many discussions have attempted to reconcile the apparent contradiction by use of the potential/actual distinction. There is a point everywhere in the sense that a magnitude is potentially divided at the point. On the other hand, the uncompletable nature of (the process of) infinity is such that any magnitude subject to successive division is never fully divided. So, there are places at which there is no point (where it is actually divided). This might seem to be a promising way to remove the contradiction; yet David Bostock has extended Zeno's arguments to show that the potential/actual distinction does not, in fact, work.⁽²¹⁾ Aristotle uses the distinction to dispute Zeno's argument -- he argues that Achilles does not actualize an infinity of points on his way to the tortoise. (263a23) Now, one way for a point to be actualized is for something to stop at it (262a21), and, in order for something to reverse direction, it must stop at, and thus actualize, the point of reversal. Bostock extends Zeno's argument to a bouncing ball in a way that actualizes an infinity of points.

But [Aristotle] was able to deny the (actual) existence of these points only by denying that they had been actualized, for Achilles was not supposed to have done anything at or to the points as he passed them. However this reply is surely not available to the revised version of Zeno's problem that I have just put forward, for the ball's motion is certainly divided into infinitely many parts by the infinitely many points which mark the top of each bounce, and these must surely be admitted to have been actualized in the course of bouncing. I conclude, then, that Aristotle does not after all have the right solution to Zeno's problem.⁽²²⁾

Aristotle himself asserts that points are not contiguous. Any object made up of points cannot be divisible at "non-points" "between" non-contiguous points. Unfortunately, between any two points there is another, to any desired degree of precision, using our usual order relation. So, between any non-contiguous points there are other points at which the object is potentially divided. We now know that the axiom of choice is equivalent to the axiom "Every set can be well ordered."⁽²³⁾ (A set is well ordered if every subset has a least element.) This axiom makes no statement about the cardinality of a set or the order under which it exhibits denseness. When it comes to the real number line, we don't know what the well-order relation is, but when so ordered, the points, separated by that order relation, would be consecutive without intervening points; but this would not be by the usual order relation, '<' (under which continuous objects are dense).

A tension pervades Aristotle's thoughts on the infinite in general and infinite divisibility in particular. One form of this tension is a conflict between the dense structure of the potentially divided or undivided model on the one hand and the discrete structure of the actually divided or exploded model on the other hand. The basic incompatibility of these two views is not discovered by Aristotle. He appears to shift back and forth between the two models using predominately syntactic-level arguments. This shift may be facilitated by his holding a view of "place" which is inconsistent with his view of "points". There are both contiguous and consecutive places, while there can't be both contiguous and consecutive points. Since there is no logical way to tell places from points aside from the definition that points go into place, the view is inconsistent at worst, ambivalent at best.

Aristotle, and his predecessors, also had an (understandably) immature understanding of infinity; he believed that, essentially, zero times infinity is zero -- whereas we now know the product to be indeterminate. Further, neither Aristotle nor his predecessors were aware that infinity could be differentiated into different "sizes" -- a distinction which could go a long way toward resolving difficulties with infinite divisibility.

In chapter VI I show that a careful analysis of the positions of atomism (page 167) and infinite divisibility (page 158) reveals that both points of view are internally self-consistent. Both perspectives coexist in a manner comparable to the wave/particle duality of modern physics. Many of Aristotle's insights are still current, but he neither proved that magnitude is infinitely divisible nor did he refute the atomists.

(Chapter 5)